macam macam simetri

Setelah dipertemuan sebelumnya telah Penulis jelaskan secara lebih detail mengenai Sifat Sifat Bangun Datar Matematika, maka sekarang tiba waktunya bagi Penulis Rumus Rumus untuk membahas secara lebih detail pula tentang Jenis dan Macam Simetri Pada Bangun Datar Matematika, karena tidak bisa dipungkiri bahwa diluar sana masih banyak Pembaca dan Pelajar yang belum begitu memahami dan belum begitu mengerti akan Simetri didalam Bangun Datar Matematika ini, padahal Materi Simetri di Bangun Datar ini penting karna sering kali muncul di Soal – Soal Ujian Sekolah dan Soal – Soal Ujian Nasional untuk Mata Pelajaran Matematika.

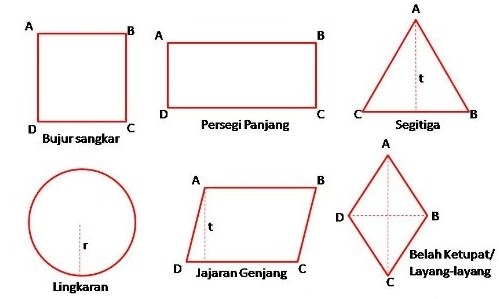
Langsung saja untuk pembahasan tentang Apa Itu Simetri Bangun Datar dan Pengertian Simetri Bangun Datar menurut wikipedia Indonesia adalah sebuah karakteristik dari suatu bidang Bangun Datar yang akan bersimetri mematuhi Operasi Simetri dan ketika diperlakukan kedalam Objek maka tidak akan muncul suatu perubahan. Selain itu kalian sebagai Pembaca dan Pelajar tentu sudah cukup memahami bahwa didalam Bangun Datar Matematika itu mempunyai Sifat – Sifat Bangun Datar, dan diantara Sifat – Sifat Bangun Datar Matematika tersebut terdapat Simetri atau sering dikatakan sebagai Simetri Bangun Datar Matematika.

Macam – Macam Simetri Bangun Datar Matematika

Kemudian didalam Macam – Macam Simetri Pada Bangun Datar Matematika terbagi menjadi Dua Macam Simetri Bangun Datar yang antara lain :

1. Simetri Lipat Bangun Datar

2. Simetri Putar Bangun Datar

Dan untuk pembahasan lengkap tentang Kedua Macam Simetri Bangun Datar Matematika tersebut, bisa kalian lihat ulasan lengkapnya dibawah ini :

1. Simetri Lipat Bangun Datar Matematika

Langsung saja didalam Pengertian Simetri Lipat Bangun Datar Matematika ini adalah banyaknya lipatan didalam Bangun Datar yang dapat membagi suatu bangun datar tersebut, sehingga bagian setengah yang ada di bangun datar matematika itu dapat menutupi setengah bagian yg lain. Kemudian perlu kalian ketahui bahwa didalam didalam Simetri Lipat Bangun Datar Matematika terdapat istilah Sumbu Simetri, dan Sumbu Simetri ini adalah garis yg dapat membagi sebuah Bangun Datar menjadi dua dan saling kongruen. Mungkin bisa kalian lihat contohnya mengenai Sumbu Simetri Pada Bangun Datar Matematika seperti dibawah ini :

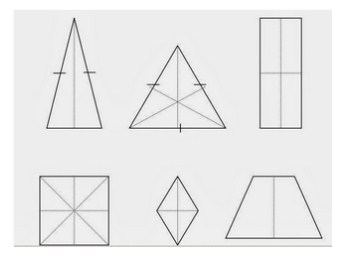
Contoh gambar diatas bisa kalian lihat bahwa Garis Putus – Putus didalam Bangun Datar Matematika diatas disebut dengan Sumbu Simetri. Hanya saja disetiap Bangun Datar Matematika tidak semuanya mempunyai Garis Putus – Putus (Sumbu Simetri) sehingga ada baiknya jika kalian bisa lebih memahami tentang Sumbu Simetri digambar diatas.

2. Simetri Putar Bangun Datar Matematika

Untuk pembahasan mengenai Macam Simetri Bangun Datar Kedua ialah Simetri Putar Bangun Datar dan Pengertian Simetri Putar Bangun Datar ini adalah bangun datar yang mempunyai sebuah titik pusat dan apabila bangun datar matematika tersebut bisa diputar kurang dari 1 putaran penuh untuk memperoleh bayangan yg tepat seperti bangun semula. Didalam Contoh Simetri Putar Bangun Datar Matematika bisa kalian lihat dibawah ini :

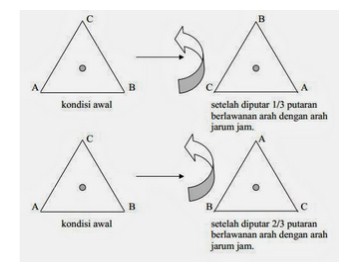
Di contoh gambar diatas, terdapat Bangun Datar Segitiga Sama Sisi dan jika Bangun Datar Matematika Segitiga tersebut diputar sebanyak 1/3 putaran yg berlawanan arah jarum jam, maka bentuk dari Bangun Datar Segitiga Sama Sisi itu akan tetap sama seperti semula. Dan jika kita putar kembali Bangun Datar Segitiga Sama Sisi itu sebanyak 2/3 putaran maka bayangannya masih tetap sama persis dengan bentuk semula, maka itu artinya Bangun Datar Segitiga Sama Sisi itu mempunyai 3 Simetri Putar.

Selain itu tentunya tidak semua Bangun Datar Matematika mempunyai Simetri Putar karena terdapat beberapa Bangun Datar Matematika yang tidak mempunyai Simetri Putar didalamnya, seperti Bangun Datar Trapesium karena Trapesium jika diputar maka hanya memperoleh bayangan seperti semula pada putaran 1 penuh sehingga hal ini bisa disimpulkan bahwa Bangun Datar Trapesium tidak mempunyai Simetri Putar sama sekali.

3. Tabel Simetri Bangun Datar Matematika

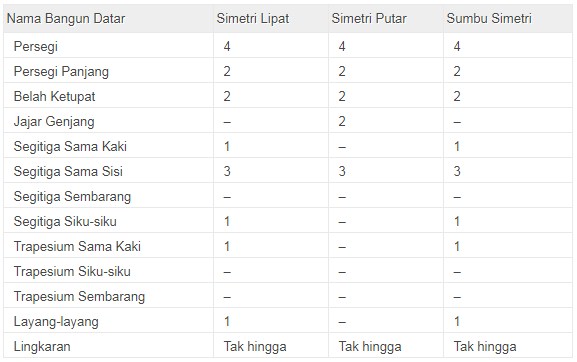
Dengan adanya Tabel Simetri Pada Bangun Datar Matematika diatas maka bisa membantu kalian sebagai Para Pembaca dan Pelajar untuk memahami tentang Bangun Datar Matematika mana saja yang mempunyai Simetri Lipat dan Simetri Putar karena sekali lagi tidak bisa dipungkiri bahwa pembahasan mengenai Simetri Bangun Datar Matematika ini cukup penting dan cukup sering keluar di Soal – Soal Ujian Mata Pelajaran Matematika.

Mungkin hanya seperti itu saja pembahasan mengenai Macam dan Jenis Simetri Bangun Datar Matematika, semoga saja apa yang telah dituliskan oleh Penulis ini bisa bermanfaat dan berguna bagi Para Pembaca Laman Website Rumus Rumus ini. Kemudian sebagai tambahan informasi saja bahwa jika kalian ingin mengetahui mengenai Rumus Bangun Datar Matematika seperti menghitung Luas dan Keliling Bangun Datar maka bisa kalian langsung menuju ke tautan tersebut karena disitu telah dibahas lengkap tentang Rumus Luas dan Keliling Bangun Datar Matematika.