perbedaan permutasi dan kombinasi

Pengertian Permutasi dan Kombinasi

Permutasi adalah banyaknya cara untuk membuat susunan dengan jumlah pada suatu anggota tertentu dari anggota-anggota suatu himpunan.
Kombinasi ialah banyaknya cara memilih anggota pada jumlah tertentu dari dari anggota-anggota suatu himpunan. Atau dengan kalimat lain kombinasi yaitu banyaknya cara membuat himpunan bagian dengan jumlah anggota tertentu dari anggota-anggota suatu himpunan.

Rumus Permutasi

Misal diketahui himpunan memiliki anggota sejumlah n, maka susunan terurut yang terdiri dari r buah anggota dinamakan permutasi r dari n, ditulis sebagai P(n,r) dimana r lebih kecil atau sama dengan n. Rumus permutasi adalah sebagai berikut.

rumus permutasi

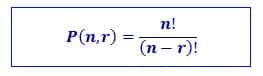
Jika r = n, Maka P (n,n) = n! (ingat 0!=1)

Contoh untuk menghitung banyaknya cara menyusun urutan dua huruf dari huruf-huruf a, b, c adalah sebagai berikut.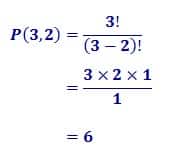

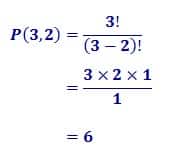
Rumus Kombinasi

Misal diketahui suatu himpunan mempunyai anggota sejumlah n, maka pemilihan r buah anggota dinamakan kombinasi r dari n, dan ditulis sebagai C (n,r) dimana r lebih kecil atau sama dengan n.
Rumus kombinasi adalah sebagai berikut

rumus kombinasi

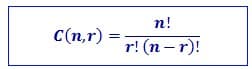
Contoh menghitung banyaknya tata cara menyusun urutan dua huruf dari huruf-huruf a, b, c

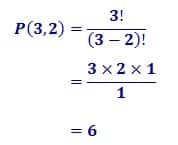
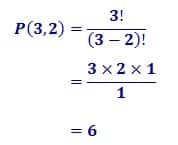
Perbedaan Permutasi dan Kombinasi

Setelah mengetahui dua rumus tentang permutasi dan kombinasi, hal yang tak kalah penting yaitu membedakan permasalahan yang termasuk dalam permutasi ataupun kombinasi. Permasalahan yang selalu muncul berupa soal cerita dan dituntut agar bisa membedakan masalah tersebut termasuk kedalam permutasi ataupun kombinasi. Hingga, tak terjadi kesalahan dalam menggunakan rumus untuk menyelesaikan masalah dalam hal tersebut.

permutasi dan kombinasi

Perhatikan dua contoh kasus berikut.

Permasalahan pertama : permasalahan permutasi
Susunan panitia yang terdiri atas ketua, sekretaris, wakil ketua dan bendahara akan dibentuk untuk mensukseskan suebuah acara. Susunan panitia tersebut akan dipilih dari 10 orang yang terpilih berdasarkan kriteria yang sudah ditentukan. Berapakah banyaknya susunan panitia yang bisa dibentuk?

Penjelasan:
susunan urutan menjadi sebuah bagian yang perlu diperhatikan. Kedudukan ketua untuk orang pertama tentu akan berbeda dengan ketua yang ditempati pada orang ke tiga. Begitu juga dengan kududukan untuk posisi yang lainnya.

Permasalahan ke dua: permasalahan kombinasi
Enam buah buku akan dipilih dari lima buku materi Matematika, tiga buku materi Fisika, dan empat buah buku materi Kimia untuk disumbangkan ke sekolah anak jalanan.
Berapakah banyaknya cara yang bisa dilakukan untuk memilih enam buku tersebut?

Penjelasan:
pemilihan buku pada urutan pertama dan kedua misalnya yaitu buku Matematika pertama dan pada buku Matematika ke dua, keduanya merupakan buku materi Matematika. Hingga, urutan tidak terlalu dipehatikan. Pada intinya, rumus permutasi dipakai untuk permasalahan yang memperhatikan urutan. Sedangkan kombinasi dipakai untuk menyelesaikan permasalahan yang tidak memperhatikan urutan.

Contoh Soal

Contoh Soal 1

Pertanyaan : 3 orang anak akan duduk bersama di sebuah bangku yang panjang. Ada berapakah cara mereka duduk bersama pada bangku tersebut?
Jawaban:
Ketiga anak akan duduk bersama, maka dipakai rumus permutasi P(3,3)
P(3,3) = 3 = 2x2x1 = 6
Maka ketiga anak tersebut bisa duduk bersama dengan 6 cara

Contoh Soal 2

Pertanyaan :  Ada berapa cara menyusun dua huruf dari sebuah kata “HIDUP”?
Jawaban:
Cara menyusun 2 huruf dari 5 huruf, maka dipakai permutasi P(5,2)
P(5,2) = (5!)/(5-2) =(5x4x3!)/(3)! = 5×4 =20
Maka cara menyusun dua huruf dari sebuah kata HIDUP adalah 20 cara